3-Point Circle & Arc Functions

See also Geometric Functions, Bulge Conversion Functions

Introduction

On this page I demonstrate a set of geometric functions which may be used to construct a circle or an arc uniquely defined by three supplied points.

Each function is provided with an accompanying test program, to show how the function may be used in an application.

Finally, I utilise my LM:3p->bulge function, taken from my set of Bulge Conversion Functions, to assemble a function which will construct a 'polyarc' (2D Polyline Arc Segment) from three supplied points.

Contents

3-Point Circle

Function Syntax (LM:3pcircle <pt1> <pt2> <pt3>)
Current Version 1.1
Donate
Arguments
Symbol Type Description
pt1, pt2, pt3 List UCS points through which to construct the circle
Returns
Type Description
List List of: (<UCS-center> <radius>) of circle

Function Description

This function will return a list of the UCS center and radius of the uniquely defined circle whose circumference passes through three supplied UCS points.

The function will return nil if the circle is undefined, such as the case if the three supplied points are collinear.

The first version of the function calculates the coordinates of the center by exploiting the geometric property that the perpendicular bisectors of any two chords of a circle will intersect at the circle center:

Select all 
;; 3-Point Circle  -  Lee Mac
;; Returns the center (UCS) and radius of the circle defined by three supplied points (UCS).

(defun LM:3pcircle ( pt1 pt2 pt3 / cen md1 md2 vc1 vc2 )
    (if (setq md1 (mapcar '(lambda ( a b ) (/ (+ a b) 2.0)) pt1 pt2)
              md2 (mapcar '(lambda ( a b ) (/ (+ a b) 2.0)) pt2 pt3)
              vc1 (mapcar '- pt2 pt1)
              vc2 (mapcar '- pt3 pt2)
              cen (inters md1 (mapcar '+ md1 (list (- (cadr vc1)) (car vc1) 0))
                          md2 (mapcar '+ md2 (list (- (cadr vc2)) (car vc2) 0))
                          nil
                  )
        )
        (list cen (distance cen pt1))
    )
)

Alternative Version

This alternative version calculates the coordinates of the center by solving the 3 simultaneous equations obtained when substituting each of the 3 supplied points into the general equation for a circle:

Select all 
;; 3-Point Circle (Cartesian)  -  Lee Mac
;; Returns the center (UCS) and radius of the circle defined by three supplied points (UCS).

(defun LM:3pcircle ( pt1 pt2 pt3 / a b c d )
    (setq pt2 (mapcar '- pt2 pt1)
          pt3 (mapcar '- pt3 pt1)
          a   (* 2.0 (- (* (car pt2) (cadr pt3)) (* (cadr pt2) (car pt3))))
          b   (distance '(0.0 0.0) pt2)
          c   (distance '(0.0 0.0) pt3)
          b   (* b b)
          c   (* c c)
    )
    (if (not (equal 0.0 a 1e-8))
        (list
            (setq d
                (mapcar '+ pt1
                    (list
                        (/ (- (* (cadr pt3) b) (* (cadr pt2) c)) a)
                        (/ (- (* (car  pt2) c) (* (car  pt3) b)) a)
                        0.0
                    )
                )
            )
            (distance d pt1)
        )
    )
)

Demonstration of Implementation of 3-Point Circle Function

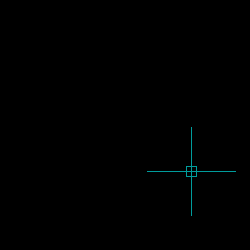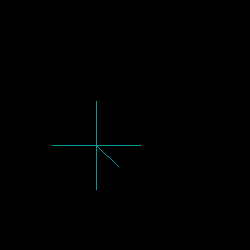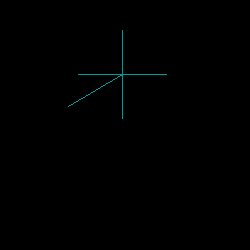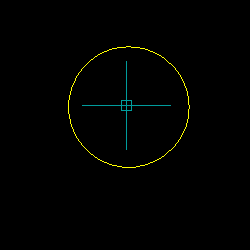
3PCircle

Example Program

Below is a program with which to test the above LM:3pcircle function.

Select all 
(defun c:3pcircle ( / lst ocs pt1 pt2 pt3 )
    (if (and (setq pt1 (getpoint "\nSpecify 1st point: "))
             (setq pt2 (getpoint "\nSpecify 2nd point: " pt1))
             (setq pt3 (getpoint "\nSpecify 3rd point: " pt2))
             (setq ocs (trans '(0 0 1) 1 0 t))
        )
        (if (setq lst (LM:3pcircle pt1 pt2 pt3))
            (entmake
                (list
                   '(000 . "CIRCLE")
                    (cons 010 (trans (car lst) 1 ocs))
                    (cons 040 (cadr lst))
                    (cons 210 ocs)
                )
            )
            (princ "\nPoints are collinear.")
        )
    )
    (princ)
)

3-Point Arc

The LM:3pcircle function shown above may also be used to construct an arc passing through the three supplied points, with the first and last supplied points forming the endpoints of the arc.

Demonstration of Implementation of 3-Point Circle Function to Construct an Arc

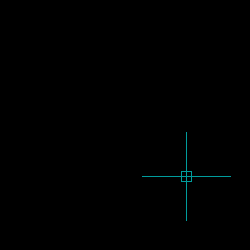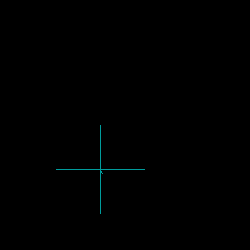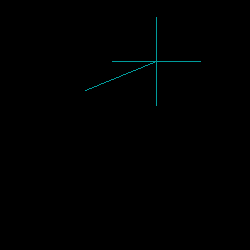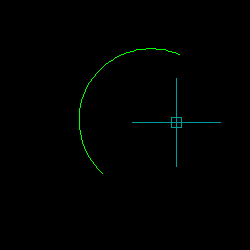
3PArc

Example Program

As demonstrated above, below is an example program showing how the LM:3pcircle function may be used to enable the construction of an arc from three supplied points.

Select all 
(defun c:3parc ( / lst ocs pt1 pt2 pt3 )
    (if (and (setq pt1 (getpoint "\nSpecify 1st point: "))
             (setq pt2 (getpoint "\nSpecify 2nd point: " pt1))
             (setq pt3 (getpoint "\nSpecify 3rd point: " pt2))
             (setq ocs (trans '(0 0 1) 1 0 t))
        )
        (if (setq lst (LM:3pcircle pt1 pt2 pt3))
            (progn
                (if (minusp (sin (- (angle pt1 pt3) (angle pt1 pt2))))
                    (mapcar 'set '(pt1 pt3) (list pt3 pt1))
                )
                (entmakex
                    (list
                       '(000 . "ARC")
                        (cons 010 (trans (car lst) 1 ocs))
                        (cons 040 (cadr lst))
                        (cons 050 (angle (trans (car lst) 1 ocs) (trans pt1 1 ocs)))
                        (cons 051 (angle (trans (car lst) 1 ocs) (trans pt3 1 ocs)))
                        (cons 210 ocs)
                    )
                )
            )
            (princ "\nPoints are collinear.")
        )
    )
    (princ)
)

3-Point Polyline Arc

Finally, below is a program which will construct a 2D Polyline (LWPolyline) with a single arc segment defined by three supplied points.

The program utilises my LM:3p->bulge function taken from my set of Bulge Conversion Functions.

Select all 
(defun c:3ppolyarc ( / ocs pt1 pt2 pt3 )
    (if (and (setq pt1 (getpoint "\nSpecify 1st point: "))
             (setq pt2 (getpoint "\nSpecify 2nd point: " pt1))
             (setq pt3 (getpoint "\nSpecify 3rd point: " pt2))
             (setq ocs (trans '(0 0 1) 1 0 t))
        )
        (entmake
            (list
               '(000 . "LWPOLYLINE")
               '(100 . "AcDbEntity")
               '(100 . "AcDbPolyline")
               '(090 . 2)
               '(070 . 0)
                (cons 038 (caddr (trans pt1 1 ocs)))
                (cons 010 (trans pt1 1 ocs))
                (cons 042 (LM:3p->bulge pt1 pt2 pt3))
                (cons 010 (trans pt3 1 ocs))
                (cons 210 ocs)
            )
        )
    )
    (princ)
)

;; 3-Points to Bulge  -  Lee Mac

(defun LM:3p->bulge ( pt1 pt2 pt3 )
    ((lambda ( a ) (/ (sin a) (cos a))) (/ (+ (- pi (angle pt2 pt1)) (angle pt2 pt3)) 2))
)

See also Geometric Functions, Bulge Conversion Functions

textsize

increase · reset · decrease

Designed & Created by Lee Mac © 2010