Sierpinski Triangle
See also Koch Snowflake, Fractals & Iterated Function Systems.
| Function Syntax | sierpinski / sierpinski3D |
| Current Version | 1.0 |
| Download | SierpinskiV1-0.lsp |
| View HTML Version | SierpinskiV1-0.html |
| Compatible with AutoCAD for Mac? | Yes |
| Compatible with AutoCAD LT? | Yes |
| Donate |
Introduction
Similar to my exploration of the Koch Snowflake, the Sierpinski Triangle (also known as the Sierpinski Gasket or the Sierpinski Sieve) is another mathematical object with fractal properties which may be generated by recursively applying a transformation to a given geometric shape.
The construction is attributed to the eponymous Polish mathematician Wacław Sierpiński, who described the object in 1915, however similar triangular pattern have been found in mosaics predating Sierpiński by 7 centuries.
Construction
A Sierpinski Triangle may be constructed in many ways - my page exploring the field of Iterated Function Systems already demonstrates an alternative way to that described on this page.
The method used by this program starts with any triangle (either defined by three arbitrary non-collinear points, or as an equilateral triangle defined by a center point and radius) and proceeds to divide the triangle into four equal parts by connecting the midpoints of each edge:
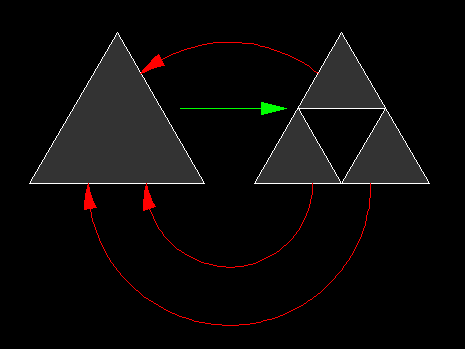
This transformation is then recursively applied to the three outer triangles, as shown by the red arrows in the above graphic.
Sierpinski Triangle
The above program will allow the user to create their own Sierpinski Triangle, and watch the fractal develop as they step through each recursive iteration.
Upon calling the sierpinski command at the AutoCAD command-line, the program will prompt the user to specify three distinct non-collinear points defining an arbitrary triangle. At this prompt the user may alternatively select the 'Center' option in order to generate the fractal from an equilateral triangle defined by a center & radius.
The user may then press ENTER or SPACE to step through each iteration, with the program reporting the number of objects which will be created by the program at each step, and an estimated time to complete the iteration, based on an extrapolation of the time taken to generate the previous iteration.

Multi-Coloured Sierpinski Triangle (just for fun!)
With a little modification to the code, we can inject some colour into each triangle:

Sierpinski Tetrahedron
The concept of the Sierpinski Triangle can be extended into the third dimension to yield a Sierpinski Tetrahedron, otherwise known as a Sierpinski Pyramid.
Here, the construction starts with a regular tetrahedron (a triangular-based pyramid), with the Sierpinski transformation applied to each face, recursively dividing each tetrahedron into four tetrahedrons, each with half the height of the original.
Such a construction may be generated in AutoCAD using the sierpinski3D command defined by the above program. Upon issuing this command at the AutoCAD command-line, the program will prompt the user to specify four distinct, non-collinear & non-coplanar points defining an arbitrary tetrahedron, or alternatively, the user may select the 'Center' option in order to generate a regular tetrahedron with a given center & radius.
The user may then step through each iteration of the construction in the same manner as the 2D command, with the program again reporting the number of objects to be created at each iteration, and an estimated time for the construction. The resulting Sierpinski Tetrahedron will be constructed from 3D Faces, as shown by the demonstration below:
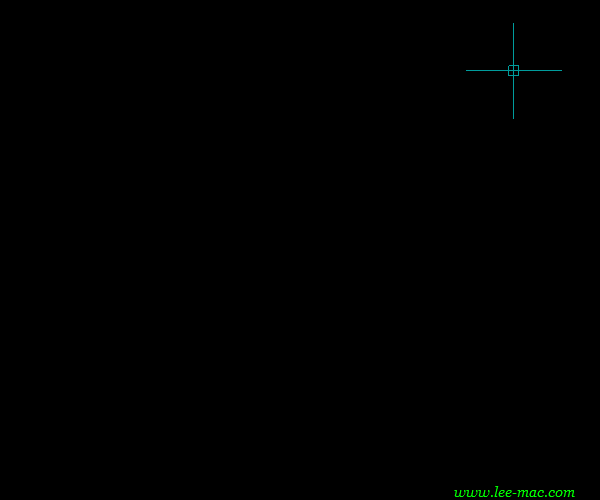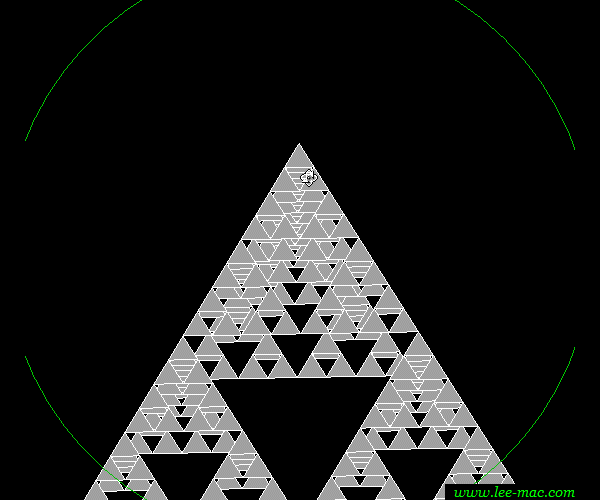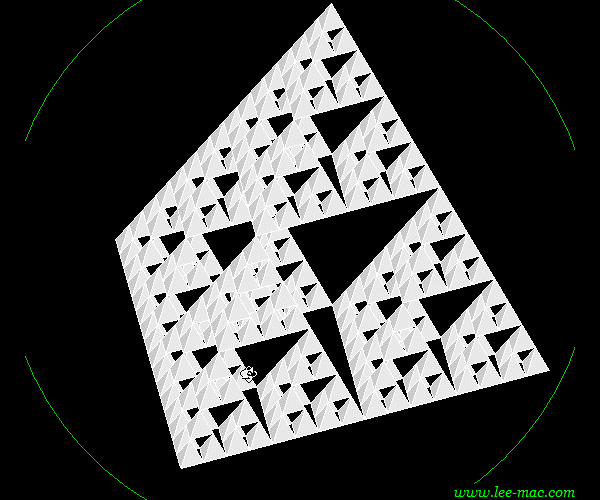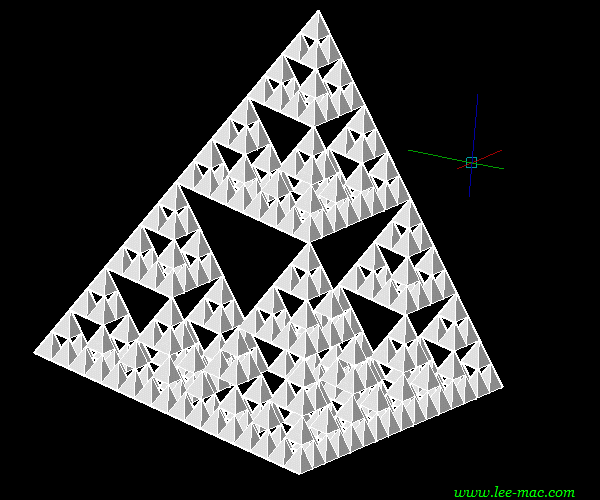
See also Koch Snowflake, Fractals & Iterated Function Systems.
Instructions for Running
Please refer to How to Run an AutoLISP Program.
