Minimum Bounding Box

Function Syntax	(LM:minboundingbox <sel> <tol>)
Current Version	1.1
Donate

Arguments
Symbol	Type	Description
sel	Selection Set	Set of objects for which to return the minimum bounding box
tol	Real	Precision of calculation: 0 < tol < 1
Returns
Type	Description
List	List of WCS points describing minimum rectangular frame bounding all objects in the selection set

Program Description

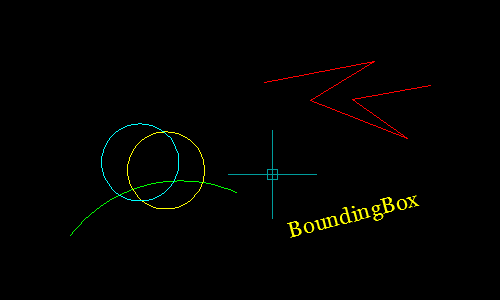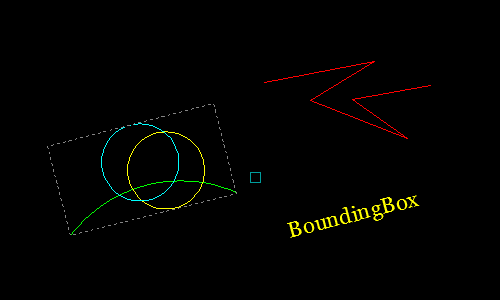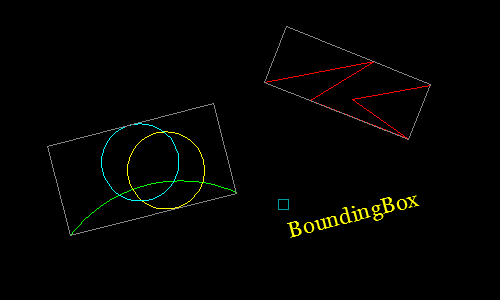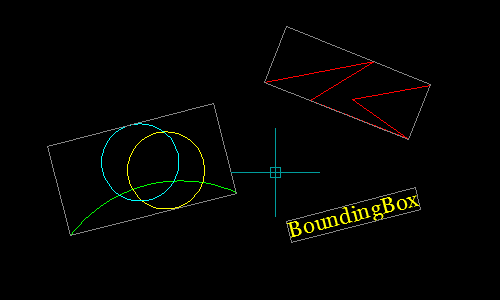
This function uses a brute-force method to determine the minimum rectangular bounding box framing all objects in a supplied selection set.

The method utilised to determine the minimum bounding box involves the function successively rotating all objects in the supplied set about a central base point (given by the initial bounding box), and calculating the area of the bounding box encapsulating all objects in the set for each rotation. Following a rotation through π radians, the coordinates of the bounding box with minimum area is returned and rotationally transformed to the set of objects at zero rotation.

The rotation increment is dependent upon the precision parameter: the smaller the value of the precision parameter, the smaller the increment and hence the more accurate the calculation; however, the calculation time is also dramatically increased for smaller precision values.

Please note that the GetBoundingBox method as used by this function is inaccurate for splines.

Select all

;; Minimum Bounding Box  -  Lee Mac
;; Returns the WCS coordinates describing the minimum bounding rectangle
;; surrounding all objects in a supplied selection set.
;; sel - [sel] selection set to process
;; tol - [rea] precision of calculation, 0 < tol < 1

(defun LM:minboundingbox ( sel tol / ang box bx1 bx2 cen idx lst obj rtn )
    (if (and sel (< 0.0 tol 1.0))
        (progn
            (repeat (setq idx (sslength sel))
                (setq obj (vlax-ename->vla-object (ssname sel (setq idx (1- idx)))))
                (if (and (vlax-method-applicable-p obj 'getboundingbox)
                         (not (vl-catch-all-error-p (vl-catch-all-apply 'vla-getboundingbox (list obj 'a 'b))))
                    )
                    (setq lst (cons (vla-copy obj) lst))
                )
            )
            (if lst
                (progn
                    (setq box (LM:objlstboundingbox lst)
                          tol (* tol pi)
                          cen (apply 'mapcar (cons '(lambda ( a b ) (/ (+ a b) 2.0)) box))
                          bx1 (* (- (caadr box) (caar box)) (- (cadadr box) (cadar box)))
                          rtn (list 0.0 box)
                          ang 0.0
                    )
                    (while (< (setq ang (+ ang tol)) pi)
                        (foreach obj lst (vlax-invoke obj 'rotate cen tol))
                        (setq box (LM:objlstboundingbox lst)
                              bx2 (* (- (caadr box) (caar box)) (- (cadadr box) (cadar box)))
                        )
                        (if (< bx2 bx1)
                            (setq bx1 bx2
                                  rtn (list ang box)
                            )
                        )
                    )
                    (foreach obj lst (vla-delete obj))
                    (LM:rotatepoints
                        (mapcar '(lambda ( a ) (mapcar '(lambda ( b ) (apply b (cdr rtn))) a))
                           '(
                                (caar   cadar)
                                (caadr  cadar)
                                (caadr cadadr)
                                (caar  cadadr)
                            )
                        )
                        cen (- (car rtn))
                    )
                )
            )
        )
    )
)

;; Object List Bounding Box  -  Lee Mac
;; Returns the lower-left and upper-right points of a rectangle bounding a list of objects

(defun LM:objlstboundingbox ( lst / llp ls1 ls2 urp )
    (foreach obj lst
        (vla-getboundingbox obj 'llp 'urp)
        (setq ls1 (cons (vlax-safearray->list llp) ls1)
              ls2 (cons (vlax-safearray->list urp) ls2)
        )
    )
    (mapcar '(lambda ( a b ) (apply 'mapcar (cons a b))) '(min max) (list ls1 ls2))
)

;; Rotate Points  -  Lee Mac
;; Rotates a list of points about a supplied point by a given angle

(defun LM:rotatepoints ( lst bpt ang / mat vec )
    (setq mat
        (list
            (list (cos ang) (sin (- ang)) 0.0)
            (list (sin ang) (cos ang)     0.0)
           '(0.0 0.0 1.0)
        )
    )
    (setq vec (mapcar '- bpt (mxv mat bpt)))
    (mapcar '(lambda ( x ) (mapcar '+ (mxv mat x) vec)) lst)
)

;; Matrix x Vector - Vladimir Nesterovsky
;; Args: m - nxn matrix, v - vector in R^n

(defun mxv ( m v )
    (mapcar '(lambda ( r ) (apply '+ (mapcar '* r v))) m)
)

Example Test Function

The following example will create a rectangular LWPolyline describing the minimum bounding box enclosing all objects in a user's selection.

Select all

(defun c:test ( / sel )
    (if (setq sel (ssget "_:L"))
        (entmake
            (append
               '(
                    (000 . "LWPOLYLINE")
                    (100 . "AcDbEntity")
                    (100 . "AcDbPolyline")
                    (090 . 4)
                    (070 . 1)
                )
                (mapcar '(lambda ( p ) (cons 10 p)) (LM:minboundingbox sel 0.01))
            )
        )
    )
    (princ)
)
(vl-load-com) (princ)

Program Demonstration

Minimum Bounding Box

Program Description

Example Test Function

Program Demonstration

Jump To: